crgtr
Zombie Eight - DFZ
Here's a great article I read by Tal Bachman (She's So High) about great guitar tone. He's got some very good points.
So, You Want a Great Guitar Sound...
Want a great rock guitar sound? Do everything "wrong". Allow me to explain.
For a variety of reasons - some of them understandable, some of them daft - many aspiring rock guitarists think that a "great guitar sound" means buying a guitar with a "hot" (high output) pickup, a large amp cranked to the max, and maybe a distortion pedal in between. But if a "great guitar sound" is one that sounds more pleasing to the human ear than other possible alternatives, what I just described is not a "great guitar sound". Here's why.
What we hear as a sound is a wave of pressure through the air. The speed, or frequency, of these waves, we measure with a unit called a hertz. A hertz tells us how frequently the wave is cycling per second. So, a wave of 500 hertz means that the sound wave is cycling at a frequency of 500 times per second.
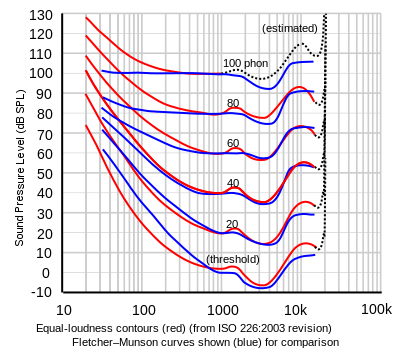
Human beings can hear sounds which range from about 20 to 20,000 hertz, but crucially, we cannot hear all those frequencies with equal ease. In fact, our ears are designed so that there is a bump in our sensitivity to frequencies around 3000 hertz (also known as 3 kilohertz or 3k, a kilohertz being equal to one thousand hertz). This makes sense, as the primary frequency in human voices is around that range. Now, virtually any sound or noise is an array of different frequencies, with some being more audible than others. But the more frequencies in 2 to 4 kilohertz range in any sound, the more we will hear that sound as harsh and unpleasant, simply because our ears are so much more sensitive to frequencies in that range.
Now, back to your guitar sound. The particular wood used to make an electric guitar will have a measurable effect on a guitar's tone, but the primary determinant of a guitar's sound is the pickup. A pickup is the device in an electric guitar which senses, or "picks up", the vibrations of the guitar strings, and converts them to an electric signal, which can then be amplified. Naturally, different kinds of pickups affect the characteristics of that signal in different ways.
One determining factor in how a pickup affects sound is the number of winds that the pickup has. (Pickups are made by winding metal wire around magnets). Essentially, the more winds a pickup has, the louder (or hotter) the output of the pickup becomes, and the less the pickup picks up high and low frequencies from the strings, and thus, the more the pickup broadcasts "mid-range" frequencies, in the - you guessed it - 2 to 4 kilohertz range. Which means, the harsher it sounds.
Further, as the output from a hot pickup is distorted, the more the signal from the string itself is clouded over by harsh, white noise (since that noise is in the same 2 - 4k range, and is therefore boosted by the pickup). This doesn't happen with low output pickups, at least nowhere near as much, because they pick up more of the highs and lows, while slighting the mid-range frequencies. In short, up to a certain point, a lower wound pickup gives you a better guitar sound. If your output is too low, you simply turn your amp up more; or if you want more volume running into the amp, so as to get a more distorted sound, you simply run your guitar through a volume pedal or volume-boosting EQ pedal. The pedal increases the guitar output without increasing the "noise"that a higher-wind, higher output pickup would have.
Does this sound too simple, or too good, to be true? It shouldn't. This is just how you get a more pleasing guitar tone, and certainly how you can get a great distorted rhythm sound through which you can still hear string clarity.
Consider one of the greatest power-chord rock songs of all time: "Won't Get Fooled Again", by The Who. Millions of people envision Townshend in the studio playing a Les Paul with souped up pickups, standing in front of a wall of Marshall amps, to get that sound. The truth is that Townshend played the song on a hollowbody Gretsch 6120 which Joe Walsh had given him, fitted with Gretsch's standard (low wind) Filtertron pickups (the same set up Brian Setzer used for his classic Stray Cats material). Townshend then ran the signal through a volume pedal and into a Fender amp, thereby distorting it. Presto - a truly awesome distorted power chord sound, which retains a lot of string clarity.
My dad, on "Takin' Care of Business", used a hollowbody Gretsch with Filtertrons as well, and got another classic dirty rhythm sound. Malcolm Young, of AC/DC, has always used Gretschs with Filtertrons for the same reason. His brother Angus plays a Gibson SG with humbuckers - but the humbuckers are also low, or "vintage", output. Add to this the fact that producer Mutt Lange (who produced "Highway to Hell", "Back in Black", and "For Those About to Rock" for them) regularly twiddles the EQ knobs so as to zap out the 3K range entirely from his mixes, and you have an explanation as to why the classic AC/DC guitars sound so good. (I should add here that while Filtertrons are great for distorted rhythm, they are less suited to lead work. They use a fairly strong magnet, which gives them that great attack, but detracts from sustain).
Speaking of lead work, consider what most historically-minded rock 'n roll aficionados and guitarists consider the greatest lead sound ever: Eric Clapton's sound on the John Mayall and the Bluesbreaker's "Beano" album. And, guess what? It was a '59 Les Paul, with relatively low output humbuckers, through a small Marshall combo amp. Clapton reportedly regularly turned his guitar's tone knob all the way down, and according to some reports, ran his guitar through a treble booster to restore some of the treble lost on the way to the amp. But even so, we're talking about a set-up which maximizes tone and string pitch, over harsh noise.
Another great lead sound was the solo on "Stairway to Heaven". People think it's a hot-rodded Les Paul through a Marshall stack. It's actually an old '59 Telecaster, outfitted with its standard (relatively low output) single coil pickups, through (by most accounts) a small Supro amplifier. Add in a tiny bit of natural room echo/reverb, and boom, there's another classic sound.
What Townshend, Page, and other pioneers of classic rock guitar sounds had was tone; and they had it, because they weren't using hot-rodded, high-output pickups to play through three different distortion pedals and gigantic stacks, boosting their noise to signal ratio. They were, for the most part, using older guitars, with lower output pickups, to get subtler, sweeter distorted sounds, which paradoxically, make their guitars sound far bigger than most modern distorted guitar sounds. And certainly, those vintage sounds were far easier to listen to - not because there is something "magic" about their age, but simply because the set-ups were, in effect, reducing frequencies in the 2 to 4 kilohertz range, and accentuating string pitch over noise.
For those interested in experimenting with achieving tone, as opposed to white-noise-style distortion, a few recommendations.
Lollar offers a great sounding low output humbucker pickup called the Low Wind Imperial. Kinman also offers spectacular sounding, lower output humbuckers. Seymour Duncan offers an Eric Johnson-designed low output humbucker as well, and while I have heard good things about that, I have never heard it myself. And then, of course, there is the Filtertron, the pickup that Townshend used for the great rhythm sound on "Won't Get Fooled Again". I suggest going to the TV Jones website if you're interested in that; they make a wide assortment of Filtertron reproductions of varying hotness. (Remember, though, that if you're looking for a lot of sustain for rock leads, a classic Filtertron may not be your best choice).
In any case, good luck with your quest to get a great guitar tone. Send me an email if you want to discuss.
So, You Want a Great Guitar Sound...
Want a great rock guitar sound? Do everything "wrong". Allow me to explain.
For a variety of reasons - some of them understandable, some of them daft - many aspiring rock guitarists think that a "great guitar sound" means buying a guitar with a "hot" (high output) pickup, a large amp cranked to the max, and maybe a distortion pedal in between. But if a "great guitar sound" is one that sounds more pleasing to the human ear than other possible alternatives, what I just described is not a "great guitar sound". Here's why.
What we hear as a sound is a wave of pressure through the air. The speed, or frequency, of these waves, we measure with a unit called a hertz. A hertz tells us how frequently the wave is cycling per second. So, a wave of 500 hertz means that the sound wave is cycling at a frequency of 500 times per second.
Human beings can hear sounds which range from about 20 to 20,000 hertz, but crucially, we cannot hear all those frequencies with equal ease. In fact, our ears are designed so that there is a bump in our sensitivity to frequencies around 3000 hertz (also known as 3 kilohertz or 3k, a kilohertz being equal to one thousand hertz). This makes sense, as the primary frequency in human voices is around that range. Now, virtually any sound or noise is an array of different frequencies, with some being more audible than others. But the more frequencies in 2 to 4 kilohertz range in any sound, the more we will hear that sound as harsh and unpleasant, simply because our ears are so much more sensitive to frequencies in that range.
Now, back to your guitar sound. The particular wood used to make an electric guitar will have a measurable effect on a guitar's tone, but the primary determinant of a guitar's sound is the pickup. A pickup is the device in an electric guitar which senses, or "picks up", the vibrations of the guitar strings, and converts them to an electric signal, which can then be amplified. Naturally, different kinds of pickups affect the characteristics of that signal in different ways.
One determining factor in how a pickup affects sound is the number of winds that the pickup has. (Pickups are made by winding metal wire around magnets). Essentially, the more winds a pickup has, the louder (or hotter) the output of the pickup becomes, and the less the pickup picks up high and low frequencies from the strings, and thus, the more the pickup broadcasts "mid-range" frequencies, in the - you guessed it - 2 to 4 kilohertz range. Which means, the harsher it sounds.
Further, as the output from a hot pickup is distorted, the more the signal from the string itself is clouded over by harsh, white noise (since that noise is in the same 2 - 4k range, and is therefore boosted by the pickup). This doesn't happen with low output pickups, at least nowhere near as much, because they pick up more of the highs and lows, while slighting the mid-range frequencies. In short, up to a certain point, a lower wound pickup gives you a better guitar sound. If your output is too low, you simply turn your amp up more; or if you want more volume running into the amp, so as to get a more distorted sound, you simply run your guitar through a volume pedal or volume-boosting EQ pedal. The pedal increases the guitar output without increasing the "noise"that a higher-wind, higher output pickup would have.
Does this sound too simple, or too good, to be true? It shouldn't. This is just how you get a more pleasing guitar tone, and certainly how you can get a great distorted rhythm sound through which you can still hear string clarity.
Consider one of the greatest power-chord rock songs of all time: "Won't Get Fooled Again", by The Who. Millions of people envision Townshend in the studio playing a Les Paul with souped up pickups, standing in front of a wall of Marshall amps, to get that sound. The truth is that Townshend played the song on a hollowbody Gretsch 6120 which Joe Walsh had given him, fitted with Gretsch's standard (low wind) Filtertron pickups (the same set up Brian Setzer used for his classic Stray Cats material). Townshend then ran the signal through a volume pedal and into a Fender amp, thereby distorting it. Presto - a truly awesome distorted power chord sound, which retains a lot of string clarity.
My dad, on "Takin' Care of Business", used a hollowbody Gretsch with Filtertrons as well, and got another classic dirty rhythm sound. Malcolm Young, of AC/DC, has always used Gretschs with Filtertrons for the same reason. His brother Angus plays a Gibson SG with humbuckers - but the humbuckers are also low, or "vintage", output. Add to this the fact that producer Mutt Lange (who produced "Highway to Hell", "Back in Black", and "For Those About to Rock" for them) regularly twiddles the EQ knobs so as to zap out the 3K range entirely from his mixes, and you have an explanation as to why the classic AC/DC guitars sound so good. (I should add here that while Filtertrons are great for distorted rhythm, they are less suited to lead work. They use a fairly strong magnet, which gives them that great attack, but detracts from sustain).
Speaking of lead work, consider what most historically-minded rock 'n roll aficionados and guitarists consider the greatest lead sound ever: Eric Clapton's sound on the John Mayall and the Bluesbreaker's "Beano" album. And, guess what? It was a '59 Les Paul, with relatively low output humbuckers, through a small Marshall combo amp. Clapton reportedly regularly turned his guitar's tone knob all the way down, and according to some reports, ran his guitar through a treble booster to restore some of the treble lost on the way to the amp. But even so, we're talking about a set-up which maximizes tone and string pitch, over harsh noise.
Another great lead sound was the solo on "Stairway to Heaven". People think it's a hot-rodded Les Paul through a Marshall stack. It's actually an old '59 Telecaster, outfitted with its standard (relatively low output) single coil pickups, through (by most accounts) a small Supro amplifier. Add in a tiny bit of natural room echo/reverb, and boom, there's another classic sound.
What Townshend, Page, and other pioneers of classic rock guitar sounds had was tone; and they had it, because they weren't using hot-rodded, high-output pickups to play through three different distortion pedals and gigantic stacks, boosting their noise to signal ratio. They were, for the most part, using older guitars, with lower output pickups, to get subtler, sweeter distorted sounds, which paradoxically, make their guitars sound far bigger than most modern distorted guitar sounds. And certainly, those vintage sounds were far easier to listen to - not because there is something "magic" about their age, but simply because the set-ups were, in effect, reducing frequencies in the 2 to 4 kilohertz range, and accentuating string pitch over noise.
For those interested in experimenting with achieving tone, as opposed to white-noise-style distortion, a few recommendations.
Lollar offers a great sounding low output humbucker pickup called the Low Wind Imperial. Kinman also offers spectacular sounding, lower output humbuckers. Seymour Duncan offers an Eric Johnson-designed low output humbucker as well, and while I have heard good things about that, I have never heard it myself. And then, of course, there is the Filtertron, the pickup that Townshend used for the great rhythm sound on "Won't Get Fooled Again". I suggest going to the TV Jones website if you're interested in that; they make a wide assortment of Filtertron reproductions of varying hotness. (Remember, though, that if you're looking for a lot of sustain for rock leads, a classic Filtertron may not be your best choice).
In any case, good luck with your quest to get a great guitar tone. Send me an email if you want to discuss.